A Kriging-Based Approach to Autonomous Experimentation with Applications to X-Ray Scattering
Citation
Noack, M.M.; Yager, K.G.; Fukuto, M.; Doerk, G.S.; Li, R.; Sethian, J.A. "A Kriging-Based Approach to Autonomous Experimentation with Applications to X-Ray Scattering"
Scientific Reports 2019,
9 11809.
doi: 10.1038/s41598-019-48114-3Summary
We demonstrate an algorithm that can be used for autonomous decision-making, allowing scientific experiments to be automated and run more optimally. Proof-of-principle experiments are demonstrated where the algorithm is used to drive an x-ray scattering beamline.
Abstract
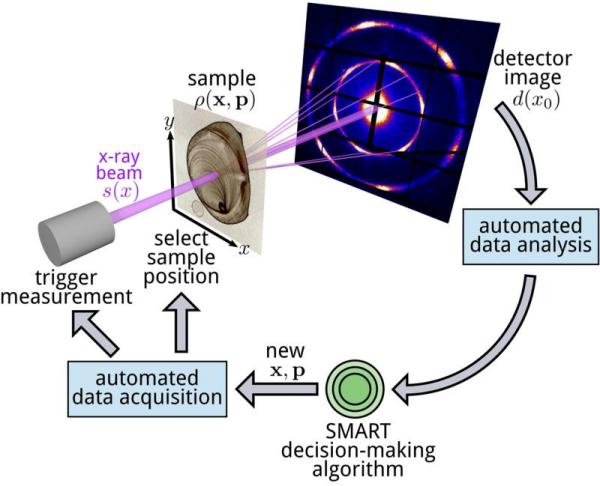
Modern scientific instruments are acquiring data at ever-increasing rates, leading to an exponential increase in the size of data sets. Taking full advantage of these acquisition rates will require corresponding advancements in the speed and efficiency of data analytics and experimental control. A significant step forward would come from automatic decision-making methods that enable scientific instruments to autonomously explore scientific problems—that is, to intelligently explore parameter spaces without human intervention, selecting high-value measurements to perform based on the continually growing experimental data set. Here, we develop such an autonomous decision-making algorithm that is physics-agnostic, generalizable, and operates in an abstract multi-dimensional parameter space. Our approach relies on constructing a surrogate model that fits and interpolates the available experimental data, and is continuously refined as more data is gathered. The distribution and correlation of the data is used to generate a corresponding uncertainty across the surrogate model. By suggesting follow-up measurements in regions of greatest uncertainty, the algorithm maximally increases knowledge with each added measurement. This procedure is applied repeatedly, with the algorithm iteratively reducing model error and thus efficiently sampling the parameter space with each new measurement that it requests. We validate the method using synthetic data, demonstrating that it converges to faithful replica of test functions more rapidly than competing methods, and demonstrate the viability of the approach in an experimental context by using it to direct autonomous small-angle (SAXS) and grazing-incidence small-angle (GISAXS) x-ray scattering experiments.

