Autonomous materials discovery driven by Gaussian process regression with inhomogeneous measurement noise and anisotropic kernels
Citation
Noack, M.M.; Doerk, G.S.; Li, R.; Streit, J.K.; Vaia, R.A.; Yager, K.G.; Fukuto, M. "Autonomous materials discovery driven by Gaussian process regression with inhomogeneous measurement noise and anisotropic kernels"
Scientific Reports 2020,
10 17663.
doi: 10.1038/s41598-020-74394-1Summary
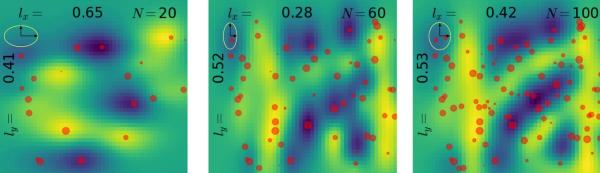
We demonstrate how advanced Gaussian process methods can be used to steer autonomous experiments. In particular, consideration of noise that varies over the parameter space, and anisotropy in characteristic lengthscales, provide improved modeling and thus improved autonomous control.
Abstract
A majority of experimental disciplines face the challenge of exploring large and high-dimensional parameter spaces in search of new scientific discoveries. Materials science is no exception; the wide variety of synthesis, processing, and environmental conditions that influence material properties gives rise to particularly vast parameter spaces. Recent advances have led to an increase in the efficiency of materials discovery by increasingly automating the exploration processes. Methods for autonomous experimentation have become more sophisticated recently, allowing for multi-dimensional parameter spaces to be explored efficiently and with minimal human intervention, thereby liberating the scientists to focus on interpretations and big-picture decisions. Gaussian process regression (GPR) techniques have emerged as the method of choice for steering many classes of experiments. We have recently demonstrated the positive impact of GPR-driven decision-making algorithms on autonomously-steered experiments at a synchrotron beamline. However, due to the complexity of the experiments, GPR often cannot be used in its most basic form, but rather has to be tuned to account for the special requirements of the experiments. Two requirements seem to be of particular importance, namely inhomogeneous measurement noise (input-dependent or non-i.i.d.) and anisotropic kernel functions, which are the two concepts that we tackle in this paper. Our synthetic and experimental tests demonstrate the importance of both concepts for experiments in materials science and the benefits that result from including them in the autonomous decision-making process.

